Copyright Derek O'Reilly, Dundalk Institute of Technology (DkIT), Dundalk, Co. Louth, Ireland.
The display on a monitor can be broken into one or more viewports (or windows). Only those characters that appear inside an open viewport should be displayed.
It is easy to determine if a point is inside or outside a viewport.
The situation with lines is more difficult, as a line can be fully inside or fully outside a viewport, or a line can be partially inside and partially outside a viewport.
The Cohen-Sutherland clipping algorithm can be used to efficiently identify lines that can be trivially accepted or rejected against a 2D viewport.

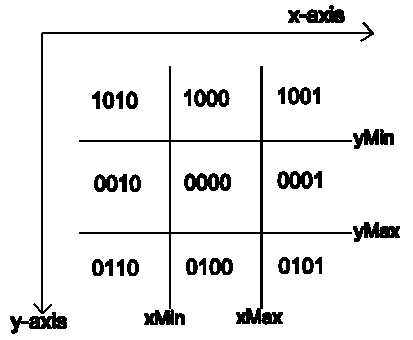
Assign to both endpoints of the line a four bit outcode based on the nine regions shown in the above diagram.
A bit in the outcode is TRUE (1) if a given relation between the point and viewport is true:
otherwise the bit is FALSE (0).
Note: That Bit 1 is the leftmost and Bit 4 is the rightmost.
In software, we can calculate the outcode as:
In hardware, if bit 1 equals 0 then the number is positive, else the number is negative.
We can calculate the outcode as:
A line can be trivially accepted if both of its end-points are in the viewport. If both end-points are in the viewport, then all bits of both outcodes == 0000. This is the case when the logical OR of the two outcodes is equal to 0000.
A line is trivially rejected if both end-points are above, below or to the same side of the viewport. Both end-points will be above, below or to the same side of the viewport if the corresponding bit in the outcode for both end-points is 1. This is the case when the logical AND of the two outcodes is NOT equal to 0000.
If the result of the logical AND is 0000, the line can neither be trivially accepted or rejected.
An iterative divide and conquer approach is used to find out if the line is to be accepted or rejected and to list the intersection points between the line and the viewport for those lines that lie partly inside the viewport.
Up to four iterations are needed to clip a line against a viewport.
For lines that are not trivially accepted or rejected we know the coordinates of the end-point inside the viewport.
Given the end-point P(x,y) inside the viewport, we can use the slope (m) formula to calculate the intersection point between the line and the viewport. The intersection is the second end-point.
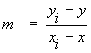
For lines that intersect the top and the bottom of the viewport we know the yI coordinate. It is equal to yMin and yMax respectively. To find xI we apply the slope formula:
![]()
For lines that intersect the left and the right of the view plane we know the xI coordinate. It is equal to xMin and xMax respectively.
![]()
As m is a floating point number, the xi and yi intersection points need to be rounded to the nearest integer number. If processing speed is more important than exact accuracy, it can be quicker to simply cast the xi and yi intersection points to int.
for each line
{
bool drawLineFlag = true;
if (!TrivialAccept())
{
m = (float)(y2 - y1) / (x2 - x1);
for each of the line's two endpoints
{
if (!TrivialReject()) // this needs to be inside the for loop
// because the original line could be
// trivially rejected or the translated
// line after the first clip could be
// trivially rejected
{
// we can use the outcode to make this if/then/else more efficient
if (y < yMin) // endpoint is above window
{
xI = x + Round((yMin - y) / m);
yI = yMin;
x = xI;
y = yI;
}
else if (y > yMax) // endpoint is below window
{
xI = x + Round((yMax - y) / m);
yI = yMax;
x = xI;
y = yI;
}
// do NOT use the outcode for this if/then/else,
// because the line's end-point might have moved as a result of the previous if/then/else
if (x < xMin) // endpoint is to the left of window
{
xI = xMin;
yI = y + Round(m * (xMin - x));
}
else if (x > xMax) // endpoint is to the right of window
{
xI = xMax;
yI = y + Round(m * (xMax - x));
}
}
else // trivial reject
{
drawLineFlag = false;
}
}
if (drawLineFlag)
{
DrawLine()
}
}
}
Just as in line drawing, it is desirable to avoid the use of floating point numbers, multiplication and division.
We can use midpoint subdivision to calculate the point of intersection between a line and the view plane.
A line's midpoint is ((x2+x1)/2,(y2+y1)/2). This can be calculated for integer coordinates with two additions and right shifts.
By continually applying this formula to that part of the line segment that intersects the view plane we home in onto the intersection point in a binary search fashion.
In order to use midpoint subdivision we must deal with only integer coordinates.
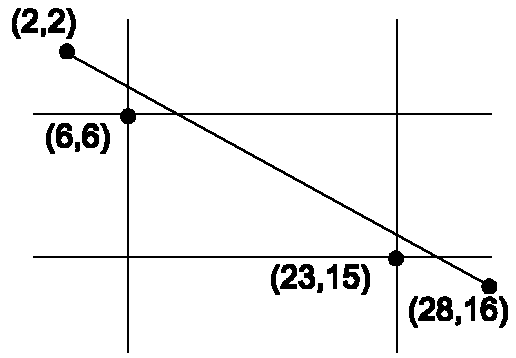
What is the result of clipping the line defined by the two end-points:
P1 = (2,2)
P2 = (28,16)
against the window defined by the two points:
top left corner = (6,6)
bottom right corner = (23,15)
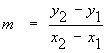
![]()
= 0.5385
Point P1 is neither trivially accepted or rejected.
P1 is above the viewport:
xI = x + (int)((yMin - y) / m) = 2 + (int)(6 - 2) / 0.5385 = 9 yI = yMin = 6 // Reset P1(2,2) to be P1(9,6) x = xI = 9 y = yI = 6
The new P1(x,y) is not to the left or to the right of the window, so no further calculations are required on it.
The intersection of P1 and the viewport is the point (9,6)
P2 is not above the viewport.
It is below the viewport:
xI = x + (int)((yMax - y) / m) = 28 + (int)(15 - 16) / 0.5385 = 27 yI = ymax = 15 // Reset P2(28,16) to be P2(27) x = xI = 27 y = yI = 15
The new P2(x,y) is not to the left of the window.
The new P2(x,y) IS to the right of the window:
xI = xMax = 23 yI = y + (int)(m * (xmax - x)) = 15 + (int)(0.5385 * (23 - 27)) = 12
The intersection of P2 and the viewport is the point (23,12)
Answer:
The intersection of P1 and the viewport is the point (9,6)
The intersection of P2 and the viewport is the point (23,12)
Copyright Derek O' Reilly, Dundalk Institute of Technology (DkIT), Dundalk, Co. Louth, Ireland.