An Overview of Ray Tracing

Ray tracing is the most popular graphics technique for rendering photo-realistic scenes.

The visual attributes of each pixel in a viewport are determined by tracing a ray from a viewing position, via the pixel, into the world coordinate system.

At its simplest, the pixel takes the colour of whichever object is struck first by the ray.

Further tracing of rays that are reflected or transmitted at the ray's intersection point with an object allows ray tracing to be used to create a large variety of optical effects.

Forward Ray Tracing

Ray Tracing techniques mimic very well the way light interacts with the real world. In the real world light is emitted from light sources. It then travels as light rays in an infinite number of directions away form the light source.

The vast majority of the rays will never be visible to a viewer looking into the scene through a view plane.

Those rays that will ultimately be visible to the viewer must first be reflected and transmitted throughout the scene, before finally being projected through the viewing plane and into the eye.

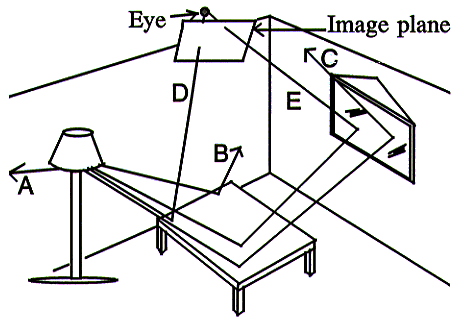
Let us take the above diagram as an example.

Light ray A travels away from the light source. Upon striking the wall it is absorbed.

Ray B strikes the table, and is reflected. It then strikes the wall and is absorbed.

Ray C is reflected off the table and the mirror before it too strikes the wall.

Ray D is reflected off the table and through the view plane into the eye.

Ray E is reflected off the table, then off the mirror and through the view plane into the eye.

By following the paths taken by these five rays we have been forward ray tracing.

Rays A, B, and C represent a sample of the vast majority of rays that will never reach the eye.

In reality, there would be an infinity of such rays.

Rays D and E, on the other hand, are rays that do reach the eye. These are the only rays that we are interested in.

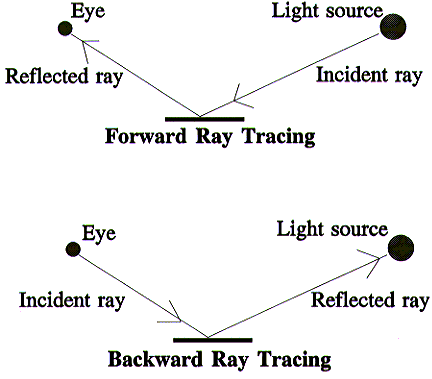
Backward Ray Tracing

Forward Ray Tracing is too inefficient a technique to implement on a computer, as only a tiny percentage of emitted rays ever reach the view plane.

Fortunately, it is possible to trace the path taken back along a ray from the eye, through the view plane, and around the scene, until it finally arrives at the light source from which it originated. Knowing the path that a ray takes and the objects that it intersects makes it possible to calculate the ray's colour. This method of tracing rays is called backward ray tracing.

Backward ray tracing guarantees that only those rays that we are interested in are traced; rays D and E in the above diagram. This is the method used by all ray tracing systems.

Because backward ray tracing is the only ray tracing method used, it is usually referred to simply as ray tracing.

Associated with backward ray tracing is some reverse terminology. When we talk about a reflected or transmitted ray, what we really refer to is the ray that caused the reflection or transmission. The direction of these rays is also reversed, as is shown in the diagram below.

Pixels and Rays

In a computer model an origin, a viewport, and a world coordinate system will take the place of the eye, the view plane and the scene respectively. To generate a perspective rendering of the scene one ray is projected from the origin through each pixel in the viewport. For parallel rendering one ray is shot through each pixel in a perpendicular direction to the view plane.

Ray Types

Rays can be divided into four classes:

pixel rays (or eye rays), which carry light directly to the eye through a pixel on a viewport on the monitor;

Although rays are divided into different classes, they are all mathematically the same. The classifications are made only as an aid to discussion.

Reflected and Transmitted Rays

When a ray intersects a point on a surface it causes a new ray to be reflected away from the surface. If the surface is not opaque then a second ray is transmitted through the surface.

Shadow and Illumination Rays

When a ray intersects a point on the surface of an object it is necessary to find out which lights in the world coordinate system are cast upon the point. The intensity of each light cast on the point will affect its colouring. In order to find out which lights do reach the point a shadow ray is sent out from the point in the direction of each of the lights in turn.

If any opaque object is positioned between the point and the light source along the path of the shadow ray, then the point is in the shadow of the object with respect to this light source. If no objects lie along the shadow ray's path, then the point is illuminated by the light source. The ray then becomes an illumination ray.

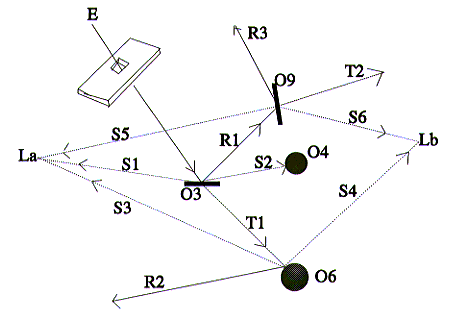
Looking at the above diagram we see that ray E intersects object O3. It then generates two shadow rays, S1 and S2. As object O4 lies in the path of shadow ray S2 we say the intersection point is in the shadow of O4 with respect to light source Lb. No objects lie in the path of shadow ray S1, so it becomes an illumination ray. This will contribute to the final colour of light leaving the intersection point back along E.

Recursive Model

If an eye ray strikes an object's surface the ray becomes an incident ray with respect to that surface. The interaction of the ray and the surface will cause a reflected ray to be generated. Depending on the surface characteristics, a transmitted ray may also be generated.

These new rays will themselves be cast in the same manner as the eye ray. Upon striking an object's surface the new rays will themselves become incident to surfaces and again a new level of reflected and transmitted rays will be generated.

This leads to a recursive model for ray tracing. The recursive model is shown in schematic form as a ray tree. The ray tree for the ray traced scene depicted on the previous diagram is shown on the next diagram.

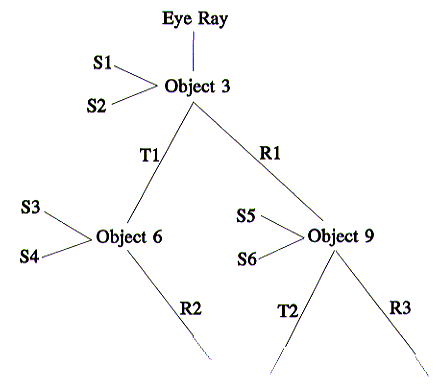
We must now ask the question "At what stage does the recursion stop?"

The usual procedure is to stop tracing if either:

When a ray leaves the world coordinate system it can be assigned a predefined background colour and traced no further.

Working out the contribution of any ray to the final colour of a ray tree is more difficult to decide. The further down its position in the ray tree, the less the contribution of any ray to the final colour. An example should help verify this. Suppose ray E was the only ray affecting a pixel (i.e. it spawned no reflected or transmitted rays), then we would take its colour as being the final colour to arrive at the top of the ray tree. However, it does spawn both a reflected and transmitted ray. Their individual contributions to the final colour must be less than that of E since E is formed by combining both together with the shadow ray S1. Now R1, the reflected ray that helped form colour E, is itself formed by combining R3 and T2, along with the shadow rays S5 and S6. Therefore, both R2 and T2 must contribute less to the final colour than does R1.

When building a ray tree, it is usual to set a contribution threshold, below which further tracing of rays stops. This technique is known as adaptive tree-depth control.