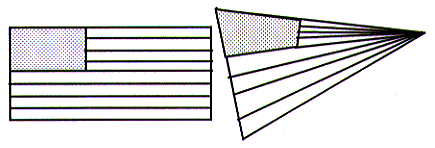
In parameterised texture mapping the whole of the texture map is mapped onto the surface of the polygon. The surface of the texture map is stretched so as to fit onto the polygon. This is shown in the diagram below.
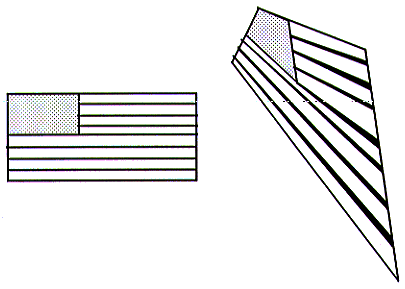
In explicit texture mapping only a part of the texture map is mapped onto the surface of the polygon. Each vertex of the polygon is explicitly assigned a coordinate in the texture map.
Explicit texture mapping is particularly useful if we are using polygons to approximate another surface. For example, if we are using polygons to approximate a globe, then we can map the globe's texture map (i.e. the map of the world) so that different parts of the texture map are mapped onto the various polygons that are being used to approximate the globe. Explicit texture mapping is shown in the diagram below.
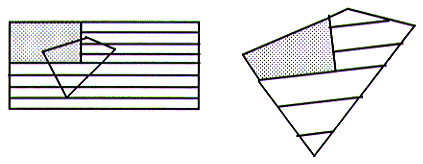
Scan line Mapping of a Four Edge Polygon onto a Texture Map
We shall now develop a texture mapping algorithm that fits into the scan line hidden surface and rendering algorithm.
The same scanline polygon texture mapping algorithm will work for both paramiterised and explicit texture mapping.
Each vertex of a polygon is assigned an x,y coordinate from the texture map.
For paramiterised texture mapping the four vertices of the polygon are assigned the four corner coordinates of the texture map.
For explicit texture mapping the four vertices are assigned coordinates within the texture map that give the desired texture map.
Once each of the four vertices is assigned a texture map coordinate, the same algorithm will work for both paramiterised and explicit texture mapping.
Linear Interpolation Along a Polygon's Edge
Given that we have assigned texture map coordinates to the two vertices that define a polygon edge, we can linearly interpolate between the two vertices' texture map coordinates to give the edge's other texture map coordinates.
If vertex V1 is assigned texture map coordinate T1 and vertex V2 is assigned T2, then the number of interpolation steps that we need equals the number of scan lines between the two vertices (i.e. V2y-V1y).
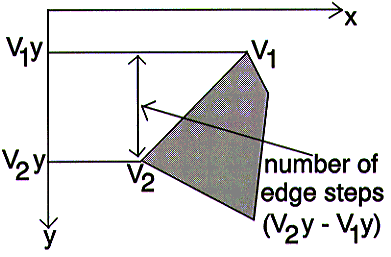
We need to map the length of the texture map edge evenly onto the V2y-V1y steps. The length of the texture map edge is equal to the distance between its two defining points (T1 and T2). We calculate the texture map edge's x and the y lengths independently. The length of the texture map edge in the x direction is T2x-T1x and the length of the texture map in the y direction is T2y-T1y.
The linear interpolation of the texture map's x coordinate as we move down one scan line is:
|
Tx+1 |
= Tx + (T2x-T1x) / (V2y-V1y) |
|
= Tx + edgeStepSizeX |
where:
· Tx is the texture map x coordinate that maps onto the polygon's edge at the current scanline.
· Tx+1 is the texture map x coordinate that maps onto the polygon's edge at the NEXT scanline.
· V1y and V2y are the polygon edge's two vertex y coordinates.
· T1x and T2x are the two texture map x coordinates that map onto V1x and V2x respectively.
NOTE: edgeStepSizeX need only be calculated once for a given polygon edge as the edge is being added to the AET.
Using the above formula, we can calculate the next edge texture map x coordinate given that we know the current edge texture map x coordinate.
We keep each polygon's edge texture map coordinate in the AET and we add the edgeStepSizeX to it each time we move down a scanline.
Similarly
|
Ty1 |
= Ty + (T2y-T1y) / (V2y-V1y) |
|
= Ty + edgeStepSizeY |
Linear Interpolation Between Two Polygon Edges
As a result of the linear interpolation along the edge of the polygon we always know the texture map's x and y coordinates for the two polygon edges that are on the current scanline.
We also know (from the AET) the two polygon edge x coordinates. These two x coordinates are used to calculate the distance between the two polygon edges. The distance between the two edges represents the number of pixels that must be coloured in. This is shown in the diagram below.
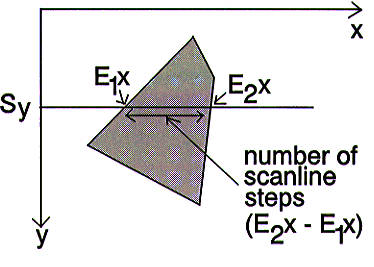
We can interpolate between the two edges texture map coordinates to fill in the pixels on the scan line.
The formula used to calculate the successive texture map x coordinates as we move across the scan line is:
|
Tx+1 |
= Tx + (T2x-T1x) / (E2x-E1x) |
|
= Tx + scanlineStepSizeX |
where:
· Tx is the current texture map coordinate (which maps onto the current x coordinate along the scanline).
· Tx+1 is the next texture map coordinate (which will be mapped onto the next x coordinate along the scanline).
· E1x and E2x are the two polygon edge x coordinates (taken from the AET).
· T1x and T2x are the two texture map x coordinates that map onto E1x and E2x respectively. These two values are got from the linear interpolation along the polygon's respective edges (as described in the last section).
NOTE: scanlineStepSizeX need only be calculated once for a given polygon and it can then be used continually as a scanline progresses across the polygon.
Similarly
|
Ty+1 |
= Ty + (T2y-T1y) / (E2x-E1x) |
|
= Ty + scanlineStepSizeY |
WORKED EXAMPLE: Texture Mapping
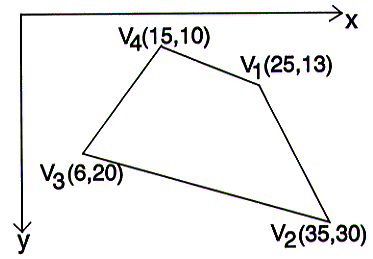
In the above diagram, we can assume that the four vertices of the polygon were assigned to the four corner points of a texture map of width 60 and height 20:
The polygon vertices are assigned to the texture map corner coordinates as follows:
|
V1 is assigned |
T1(0,0) |
|
V2 |
T2(0,20) |
|
V3 |
T3(60,20) |
|
V4 |
T4(60,0) |
Q1) For each of the four edges, by how much does the texture map's coordinate change at each new scanline? (i.e. find edgeStepSizeX and edgeStepSizeY for each of the four edges).
Q2) What coordinates of the texture map will be displayed along the polygon edge V4V3?
Q3) What coordinates of the texture map will be displayed on scanline y=15?
ANSWER Q1)
The equivalent texture map coordinate along any edge of the polygon can be got by linear interpolation between the two vertex's equivalent texture map coordinates.
The edge V4V3 maps across the top of the texture map from the coordinates 60,0 to 60,20
|
edgeStepSizeX |
= (T3x-T4x) / (V3y-V4y) |
|
= (60-60) / (20-10) |
|
|
= 0 |
|
edgeStepSizeY |
= (T3y-T4y) / (V3y-V4y) |
|
= (20-0) / (20-10) |
|
|
= 2 |
The x and y stepSize for each of the other three edges are calculated similarly:
Edge V4V1
|
edgeStepSizeX |
= (0 - 60) / (13-10) |
|
= -20 |
|
edgeStepSizeY |
= (0-0) / (13-10) |
|
= 0 |
Edge V1V2
|
edgeStepSizeX |
= (0-0) / (30-13) |
|
= 0 |
|
edgeStepSizeY |
= (20-0) / (30-13) |
|
= 1.17647 |
Edge V3V2
|
edgeStepSizeX |
= (0-60) / (30-20) |
|
= -6 |
|
edgeStepSizeY |
= (30-30) / (30-20) |
|
= 0 |
ANSWER Q2) What coordinates of the texture map will be displayed along the polygon edge V4V3?
We use the linear interpolation along a polygon's edge formula to calculate the texture map's coordinates at each position along the polygon's edge. The formula is:
Tx+1 = Tx + edgeStepSizeX
Ty+1 = Ty + edgeStepSizeY
We know:
· from "Q1)" that:
edgeStepSizeX = 0
edgeStepSizeY = 2
· V4 was assigned texture map coordinate T4(60,0).
This means:
· the first Tx value will be 60;
· the first Ty value will be 0.
The table below shows the texture map coordinates that map onto the polygon edge V4V3.
|
Scanline |
Texture Map Coordinates |
|
|
Y |
X |
Y |
|
10 |
60 |
0 |
|
11 |
60 |
2 |
|
12 |
60 |
4 |
|
13 |
60 |
6 |
|
14 |
60 |
8 |
|
15 |
60 |
10 |
|
16 |
60 |
12 |
|
17 |
60 |
15 |
|
18 |
60 |
16 |
|
19 |
60 |
18 |
|
20 |
60 |
20 |
ANSWER Q3) What coordinates of the texture map will be displayed on scanline y=15?
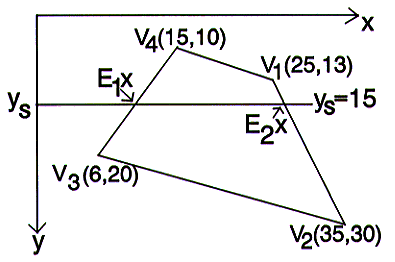
Scanline y=15 is shown in the above diagram. It cuts through edges V4V3 and V1V2.
In a program, the two polygon edge x coordinates and the two texture map edge coordinates that they map onto would be contained in the AET.
They are:
|
E43x |
= 11 |
Rounded from 10.5 |
|
E12x |
= 26 |
Rounded from 26.17647 |
|
T43x |
= 60 |
|
|
T43y |
= 10 |
|
|
T12x |
= 0 |
|
|
T12y |
= 2 |
Rounded from 2.3529 |
where:
· E43x is the x coordinate along the edge V4V3 that lies on the scanline y=15.
· E12x is the x coordinate along the edge V1V2 that lies on the scanline y=15.
E43x = 11 and E12x = 26 means that between the two polygon edges, the scanline y=15 passes through the pixels whose x coordinates are 11 to 26 inclusive.
All the pixels between the two polygon edges on the scanline y=15 will have the same y coordinate (y=15).
Calculation of the scanline step size
|
ScanlineStepSizeX |
= (T12x-T43x) / (E12x-E43x) |
|
= (0 - 60) / (26 - 11) |
|
|
= -60 / 15 |
|
|
= -4 |
|
scanlineStepSizeY |
= (T12y-T43y) / (E12x-E43x) |
|
= (2 - 10) / (26-11) |
|
|
= -8 / 15 |
|
|
= -0.53333 |
The table below shows the texture map coordinates that map onto the polygon between the edges V4V3 and V1V2 along the scanline y=15.
|
Scanline |
Texture Map Coordinates |
||
|
X |
X |
Y (Actual) |
Y (Rounded) |
|
11 |
60 |
10.00 |
10 |
|
12 |
56 |
9.466 |
9 |
|
13 |
52 |
8.933 |
9 |
|
14 |
48 |
8.4 |
8 |
|
15 |
44 |
7.866 |
8 |
|
16 |
40 |
7.3333 |
7 |
|
17 |
36 |
6.8 |
7 |
|
18 |
32 |
6.266 |
6 |
|
19 |
28 |
5.7 |
6 |
|
20 |
24 |
5.2 |
5 |
|
21 |
20 |
4.666 |
5 |
|
22 |
16 |
4.133 |
4 |
|
23 |
12 |
3.6 |
4 |
|
24 |
8 |
3.066 |
3 |
|
25 |
4 |
2.533 |
3 |
|
26 |
0 |
2 |
2 |
Scan line Mapping of a Three Edge Polygon onto a Texture Map
We can apply the algorithm described above to perform explicit texture mapping for polygons with ANY number of edges.
However, for paramiterised texture mapping, we need to customise the algorithm depending on the number of edges the polygon contains.
A simple solution for performing paramiterised texture mapping on a three edge polygon is to pass to the texture mapping algorithm a four edged version of the polygon. This is done by assigning an extra vertex that co-incides with one of the polygon's existing vertices. The fourth edge will be zero in length.
The vertex chosen to be doubled up will affect how the texture map maps onto the polygon.
In the diagram below, the polygon vertex that maps onto the texture map's top left corner has been doubled up.
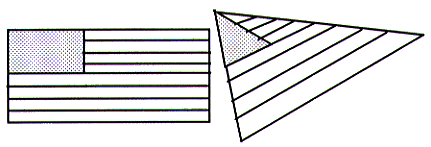
In the diagram below, the polygon vertex that maps onto the texture map's bottom right corner has been doubled up.