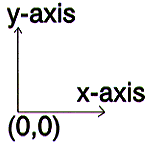
Copyright Derek O'Reilly, Dundalk Institute of Technology (DkIT), Dundalk, Co. Louth, Ireland.
Three different coordinate systems are used throughout these notes: two 2D conventions and one 3D convention.
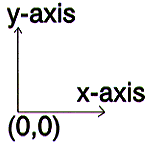
It is intuitive for humans to assign the bottom left corner of a page as the origin and to have the y-axis increase up the page, as shown in the diagram to the right.
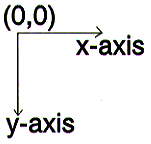
Unfortunately, computer monitors assign the top left corner as the origin and have the y-axis increase down the monitor, as shown in the diagram to the right.
The two 2D coordinate systems are used in different sections of the text with the objective of aiding clarity.
To invert the monitor's coordinate system so that it originates at the bottom left corner and has its y-axis increasing up the monitor, perform the following calculation immediately prior to displaying any point on the monitor:
ydisp = ymax - y
where:
There are two 3D coordinate systems: left-handed and right-handed.
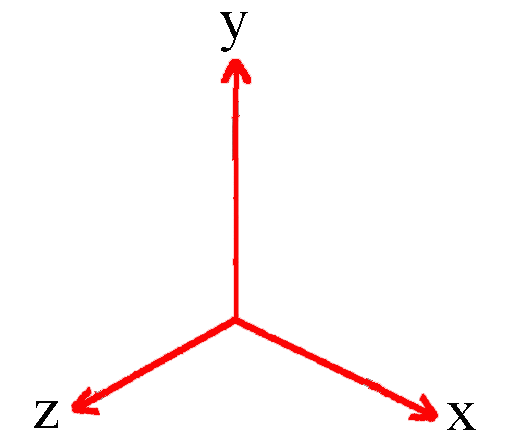
Usng the Left Hand Rule, the z-axis increases into the page. This coordinate system is shown in the diagram below.
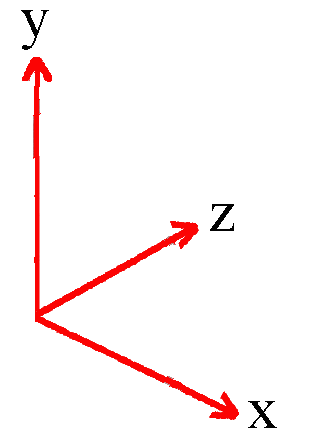
Using the Right Hand Rule, z-axis increases out from the page. This coordinate system is shown in the diagram below.
The direction below shows how you can use your left or right hand to identify the direction of the of the three principle axes.
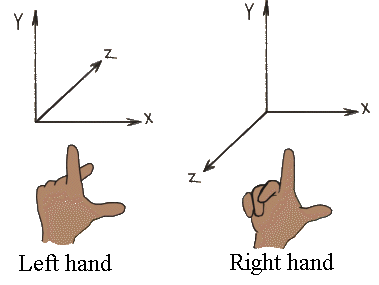
In both the Left Hand Rule and the Right Hand Rule the:
In these notes, we only use the Left Hand Rule. It is important to be aware that different text books will use either the the Left Hand Rule or the Right Hand Rule.
In the Left Hand Rule, the direction of rotation about any of the three axes is anti-clockwise around the positive axis. If you imagine your left hand being clenched around the axis with your thumb pointing in the positive direction of the axis, then your four clenched fingers point in the direction of rotation about the axis.
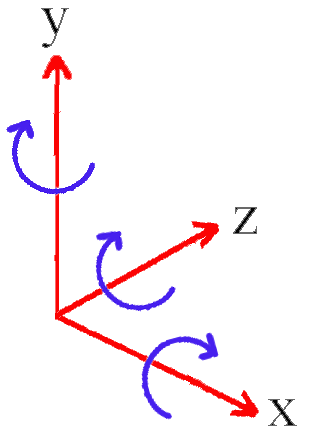
Positive rotations about the:
For these notes, we do not need to know the direction of rotation for the Right Hand Rule.
The direction of the positive z-axis is dependent on whether we are using the Left Hand Rule or the Right Hand Rule. In these notes we use the Left Hand Rule. In the Left Hand Rule, the positive z-axis goes into the page and in the Right Hand Rule, the positive z-axis comes out from the page. Conversion between a right handed and left handed coordinate system is achieved by multiplying each contol point by the matrix:
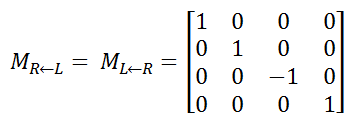
In computer graphics we often need to calculate the sin, cos or tan of an angle.
For a right angled triangle, we can easily calculate these figures:
In 3D graphics, we note that, for any plane that is parallel to any of the three principle axes, we can use the same right angled triangle rules. A plane that is parallel to the:
Therefore, for planes that are parallel to any of the three principle axes, we can use the 2D right angled triangle rules to calculate angles in 3D.
A vector has a magnitude and a direction. A vector is normally denoted by placing an arrow overhead or by using an underline, as shown below:
![]() or ab.
or ab.
A vector can be calculated from two points, using the formula below:
ab = b - a
For example, if a(3,7,10) and b(5, 3, 8) are two points, then: ab = b - a = (5, 3, 8) - (3,7,10) = (2, -4, -2)
The ordering of the two points is important, as it gives the direction of the vector. For example, the vector ba, which is (-2, 4, 2), faces in the opposite direction to ab.
The lenght of a vector is denoted by ||a|| (or less commonly by |a|)
It is equal to the square root of the sum of the squares of the elements of the vector.
For example, if a = (2, -4, -2), then
||a|| = √(2² + -4² + -2²)
= √(4 + 16 + 4)
= 4.899
A unit vector is a vector that has a length of 1. It is denoted by
![]()
It is calculated by dividing the elements of the vector by the length of the vector, as shown below:
![]()
For example, the unit vector, â, of the vector (2, -4,-2) is â = (2, -4, -2) / 4.899 = (0.4082, -0.8165, -0.4082)
The dot product can be used to calculate the cosine of the angle between two unit vectors.
The dot product of two unit length vectors a and b (sometimes called the inner product or the scalar product) is denoted by a • b and is defined as:
a • b = ||a|| ||b|| cosθ
If both a and b are unit vectors then
a • b = ||a|| ||b|| cosθ
= ||1|| ||1|| cosθ (NOTE: Both a and b MUST be unit vectors)
= cosθ
To calculate the dot product for two unit length vectors a and b we multiply each element in a by its equivalent in b and add the results together.
a • b = ax * bx + ay * by + az * bz
For example, find the cos of the angle between the two
unit directional vectors (1, 0, 0) and (0, 1, 0)?
a • b = ax * bx + ay * by + az * bz
= 1*0 + 0*1 + 0*0
= 0
We know that this is correct, as the cos of 90º is 0.
The cos is identical for both of the angles between two unit vectors. Therefore, the dot product is the same.
In the diagram below:
dot product of α = dot product of β
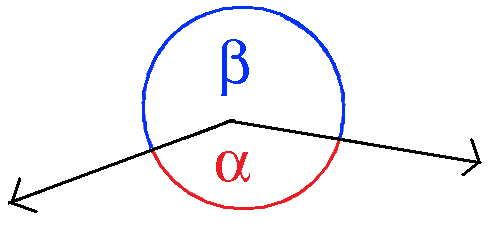
Note that, for simplicity, usually only one angle is shown in text books and other reference material.
What is the cos of the angle between the vectors ba and bc where a = (5, 5, 0), b = (1, 1, 0) and c = (8, 1, 0)?
ba = (5, 5, 0) - (1, 1, 0)
= (4, 4, 0)
Unit vector = ab / |ab|
= (4, 4, 0) / √(4² + 4² + 0 ²)
= (4, 4, 0) / 5.6569
= (0.7071, 0.7071, 0)
bc = (8, 1, 0) - (1, 1, 0)
= (7, 0, 0)
Unit vector = bc / |bc|
= (7, 0, 0) / √(7² + 0² + 0²)
= (7, 0, 0) / 7
= (1, 0, 0)
Dot Product = 0.7071 * 1 + 0.7071 * 0 + 0 * 0
= 0.7071
Cos of the angle is 0.7071 (which means the angle is 45º)
The surface normal for any surface is the directional vector that is perpendicular to the surface.
The surface normal always points away from the surface.
The surface normal is usually given as a unit directional vector.
For a plane, the surface normal is the same at every point. For a sphere the surface normal for any point is found by following the radius line through that point.
The result of the cross product of two vectors is a vector. The cross product, denoted a × b, is a vector that is perpendicular to both a and b. The cross product is also called the vector product or outer product. If we use two adjacent edges of a polygon in 3D space, then the cross product generates the surface normal of the polygon.
NOTE: The two input vectors used to calculate a cross product DO NOT have to be unit vectors.
However, in order to use the vector that results from a cross product within computer graphics, we usually need to convert it into a unit vector.
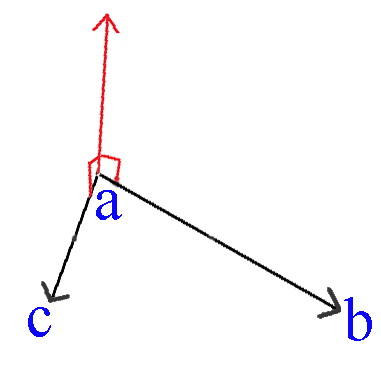
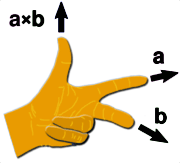
Using the Left Hand rule, the cross product of two vectors ab × ac is shown below.
You can use your left hand to determind the direction of the normal vector that is created by the cross product.
The cross product is calculated using the formula below:
a × b = (aY*bZ - aZ*bY, aZ*bX - aX*bZ, aX*bY - aY*bX)
where the:
For example, given two vectors, a = (1,2,3) and b = (4,5,6). What is the cross product of these two vectors?
a × b = (1, 2, 3) × (4, 5, 6)
= ((2*6 - 3*5), (3*4 - 1*6), (1*5 - 2*4))
= (-3, 6, -3)
Converting this vector into a unit vector would give:
= (-3/√54, 6/√54, -3/√54)
= (-0.4082, 0.8165, -0.4082)
Cross products are not commutative. Therefore, the ordering of vectors ab and ac is important. If you switch the ordering of vectors ab and ac, then the cross product results in the normal vector that points in the opposite direction. The diagram below showns ac × ab.
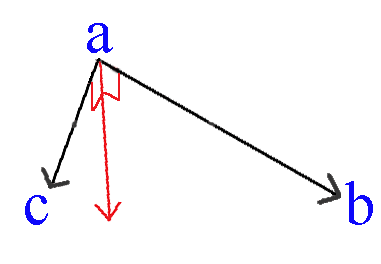
For example, given two vectors, a = (1,2,3) and b = (4,5,6). What is b × a?
b × a = ((5*3 - 6*2), (6*1 - 4*3), (4*2 - 5*1))
= (3, -6, 3)
Converting this vector into a unit vector would give:
= (3/√54, -6/√54, 3/√54)
= (0.4082, -0.8165, 0.4082)
We can see from the previous two examples that a × b = -(b × a)
For example, given two vectors, a = (1,2,3) and b = (4,5,6). What is -a ×b?
-a × b = (1, 2, 3) × (4, 5, 6)
= ((-2*6 - -3*5), (-3*4 - -1*6), (-1*5 - -2*4))
= (3, -6, 3)
Converting this vector into a unit vector would give:
= (3/√54, -6/√54, 3/√54)
= (0.4082, -0.8165, 0.4082)
We can see from the previous three examples that a × b = -(b × a ) = -(-a × b)
The Left Hand Rule determines the direction of the normal vector that results from a cross product within a left handed coordinate system.
The diagram below shows ab × ac
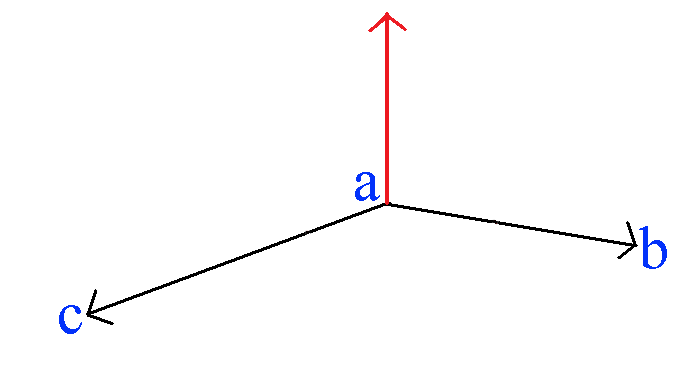
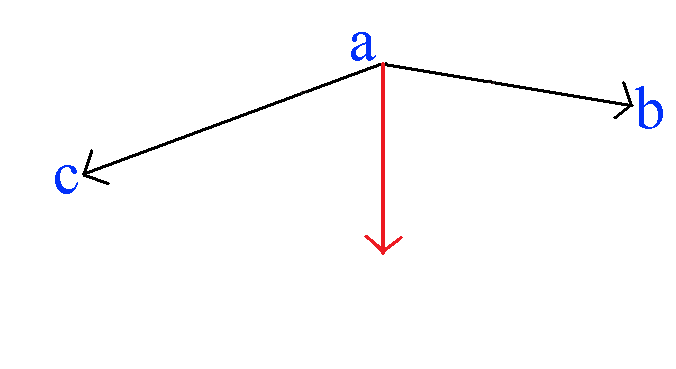
Switching the direction of the vector ab to its inverse, ba results in the cross product being inverted.
The diagram below shows ac × ab
Copyright Derek O' Reilly, Dundalk Institute of Technology (DkIT), Dundalk, Co. Louth, Ireland.