Copyright Derek O'Reilly, Dundalk Institute of Technology (DkIT), Dundalk, Co. Louth, Ireland.
In computer graphics, each colour is represented as a red, green and blue intensity.
When a light ray strikes a point on a surface, the light ray will undergo changes in colour and direction.
A rendering equation is used to colour a scene that is being displayed on a 2D viewport. The rendering formula is applied to a modeled scene when the scene is being projected onto a 2D viewport. The rendering equation is independent to the method of modelling.
Rendering equations range from those that produce very simple, but non-realistic looking, images up to those that produce complex, photo-realistic, looking images.
The interaction of the light ray and the point will cause the light ray to be reflected away from, and refracted into, the surface. The reflection and refraction is broken down into four classes:
We shall only deal with reflection of light.
The amount of influence of each effect is dependent upon the surface material and the wavelength of the light ray. Red, green and blue light will each interact independently with a surface.
If you stand back at an angle to the left and look in a mirror you will see objects, such as a chair, that are at an equal angle but to the right of the mirror. You can see the chair because light rays coming from the chair are specularly reflected by the mirror into your eyes. A light ray coming from the chair barely interacts with the mirror. The ray strikes the mirror and is reflected away. It retains the colour it had when it struck the mirror; that of the chair.
If, instead of a mirror, we were to look at a shiny piece of metal, such as copper, we would still see the chair. However, now the image would contain some copper colouring. The light ray has absorbed some of the copper's colour.
If we place a non-shiny surface, such as a piece of paper in the place of the mirror, we see only the colour of the paper. The light ray travelling from the chair was almost fully absorbed by the paper.
The colour of the reflected light ray, therefore, is dependent on the surface characteristics.
Similarly, all incident light rays interact with a surface before they are reflected and refracted.
We shall restrict our discussion to a medium quality scan-line compatible rendering equation that deals with reflection of light, but not with refraction of light.
A colour light ray is actually made up of three rays: one for each of the red, green and blue component.
When implementing the rendering equation the red, green, and blue rays are processed independently of each other. We must apply the rendering equation to the red, green and blue ray in turn.
A FOR LOOP is used to do this.
Ip is used to denote the intensity of the primary colour on the surface of an object that is being rendered. Ip is the increment parameter in the for loop.
The colouring of any surface point being rendered is influenced by four factors: Il, Is, Id and Ia, where:
NOTE:We cannot implement specularly and diffusely refracted light with the scanline algorithms that we are deriving.
A scene will contain one or more light sources of varying colours. These lights can be either point or distributed sources.
A point source is similar to a normal light bulb. We can assume that all of its light rays come from one point. For such a light source we will need to know its origin and its colour.
A distributed light source is like a fluorescent light. We model such a light source by using a number of point light sources.
When we shine an intense light onto a shiny surface we can see the effects of specular reflection: a highlight, which is the colour of the light source is produced on the surface.
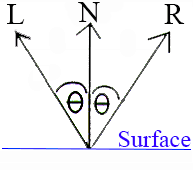
When an incident light ray strikes a flat, shiny surface, it is specularly reflected away from the surface. Specular reflection is shown in the diagram below.

The angle between the surface normal (N) and the incident light ray (L) is called the angle of incidence. We denote it as θI. The angle between the surface normal and the reflected light ray (R) is called the angle of reflection, denoted θR.
For a perfect mirror surface, the angle of reflection is equal to the angle of incidence.
We can use the cosθ to calculate point of intersection of the opposite line (i), where the hypotenuse line (L) and the adjacent line (N) of the a right angled triangle are of equal length. Normally, we shall make both L and N unit vectors.
i = N(cosθ) = N(L.N)
The diagram below shows the scaling effect that cosθ has on N. As the cosθ increases, i decreases.
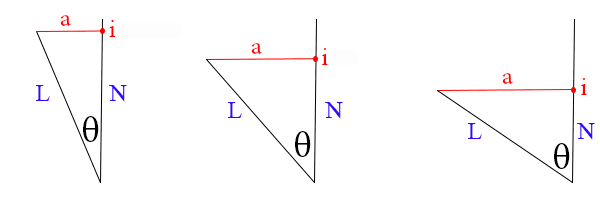
From the diagram above, if L and N are unit vectors:
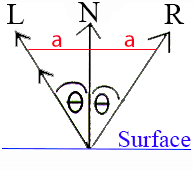
R = N(L . N) + a (1) and L + a = N (L . N) (2) From (2) a = N(L.N) - L Substituting into equation (1) R = N(L.N) + N(L.N) - L R = 2N(L.N) - L
Calculating the normalized vectors:
Given:
an incident point light source at position (-4, 2, 0),
a point on a polygon at position (0, 0, 0),
a polygon normal vector of N = (0, 1, 0).
What is the reflected vector, R?
L = (-4, 2, 0) - (0, 0, 0)
= (-4, 2, 0)
Unit direction vector of L = (-0.8944, 0.4472, 0)
L.N = (-0.8944, 0.4472, 0) • (0, 1, 0)
= 0.4472
R = 2N(L•N) - L
= 2 *(0, 1, 0) * 0.4472 - (-0.8944, 0.4472, 0)
= (0, 0.8944, 0) - (-0.8944, 0.4472, 0)
= (0.8944, 0.4472, 0)
Specularly reflected light rays travel out in different directions with unequal intensities. The reflected rays are most intense along the path of the reflected ray. There is a rapid fall-off in intensity along all other ray paths.
For a perfect reflector, light rays emanating from the light source are only reflected along the angle of reflection. This means that the viewer must be on the path of the reflected light ray in order to see the colouring effect of the incident ray.
For a non-perfect reflector, the intensity of light that is reflected along the viewing ray:
The fraction of light that is specularly reflected, called the specular reflectance coefficient, is denote W(θ). Normally, W(θ) is approximated by a constant, ks (ks must be in the range 0..1), which is set experimentally so as to produce aesthetically pleasing results. Shiny surfaces have a high value for ks and matt surfaces have a low value for ks.
Associated with ks is another surface characteristic, n (n must be ≥ 0). n is the specular reflection highlight coefficient. n was first developed by Phong Bui-Tuong.
n is used to exert control of the highlights on a surface. Matt surfaces, which do not produce sharp highlights, will have low values for n. Very shiny surfaces will have a large value for n, generating sharp highlights on the surface.
If n is 1, we get very spread out highlights. As n increases the highlight becomes increasingly sharper. If n is about 150 (or larger) we get mirror-like surfaces.
Phong Bui-Tuong approximated the intensity of the reflected light that is visible to the viewer as being (cosα)n, where α is the angle between the reflected ray and the viewer ray, as shown in the diagram below.
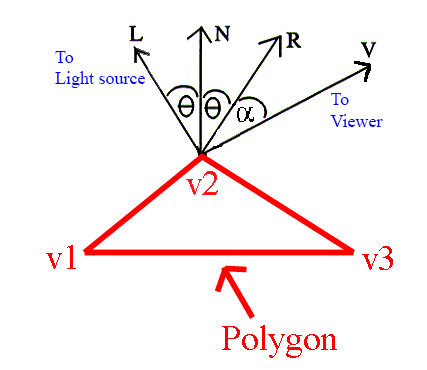
From the diagram, we can see that the calculation of V is:
V = point of viewer – point of intersection.
The formula (cosα)n reflects the rapid fall-off in intensity of light as the angle between the incident ray and the viewing ray increases.
The rendering equation (for specular reflection) is:
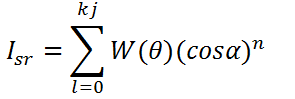
OR
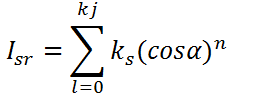
Replacing cosα with dot product
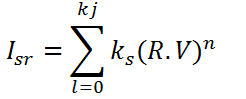
Given:
A clockwise defined polygon that has three
vertices v1(5, 0, 0), v2(0, 0, 0) and v3(5, 0, 5)
a light source that is at location l(-10, 10, 0) and
a viewpoint that is at location v(20, 5, 0)
For the point (0, 0, 0) on the polygon's surface, find:
(A) cos θ
(B) cos α
(A) Calculating cos θ
(i) Calculate the unit directional incident light vector, L.
The two points that define L are (-10, 10, 0) and (0, 0, 0)
L = b - a
= (-10, 10, 0) - (0, 0, 0)
= (-10, 10, 0)
The length of the L is √(10² + -10 ² + 0 ²) = 14.1421
Therefore the unit vector i the direction of L is (10, -10, 0) / 14.1421
|L| = (-0.7071, 0.7071, 0)
(ii) Calculate the unit normal directional vector to the polygon.
Use the cross product to find the normal to the polygon.
a = V3 - V2 = (5, 0, 5) - (0, 0, 0)
= (5, 0, 5)
b = v1 - v2 = (5, 0, 0) - (0, 0, 0)
= (5, 0, 0)
a × b = (aY*bZ - aZ*bY, aZ*bX - aX*bZ, aX*bY - aY*bX)
= ((0*0 - 5*0), (5*5 - 5*0), (5*0 - 0*5))
= (0, 25, 0)
The length of the normal vector, N, is √(0² + 25² + 0²) = 25
Therefore the unit normal vector, N, is (0, 25, 0) / 25 = (0, 1, 0)
|N| = (0, 1, 0)
(iii) Calculate cos θ
Use the dot product to calculate cos θ
L•N = cos θ
L•N = (-0.7071, 0.7071, 0) • (0, 1, 0)
L•N = ax * bx + ay * by + az * bz
= -0.7071*0 + 0.7071*1 + 0*0
= 0.7071
ANS (A) cos θ = 0.7071
(B) Calculating cos α
(i) Calculate the reflected vector R
R = 2 N (L•N) - L
= 2 * (0, 1, 0) * 0.7071 - (-0.7071, 0.7071, 0)
= (0, 2 , 0) * 0.7071 - (-0.7071, 0.7071, 0)
= (0, 1.414, 0) - (-0.7071, 0.7071, 0)
= (0.7071, 0.7071, 0)
Length of the unit reflected vector, R = √(0.7071² + 0.7071² + 0²) = 1
|R| = (0.7071, 0.7071, 0)
(ii) Calculate the unit directional viewpoint vector, V
V = (20, 5, 0) - (0, 0, 0)
= (20, 5, 0)
Length of the unit viewpoint vector, V = √((20)² + (5)² + 0²) = 20.6155
|V| = (20, 5, 0) / 20.6155
= (0.9701, 0.2425, 0)
(iii) Calculate cos α using dot product
cos α = V•R
V•R = (0.9701, 0.2425, 0) • (0.7071, 0.7071, 0)
= 0.9701*0.7071 + 0.2425*0.7071 + 0*0
= 0.6860 + 0.1715 + 0
= 0.8575
ANS cos α = 0.8575
Diffuse reflection is caused when an incident light ray is absorbed upon striking a surface. Light rays are re-radiated away from the surface point as diffusely reflected light rays.
The colouring of the diffusely reflected light rays is dependent on:
Diffusely reflected light rays travel out in all directions with equal intensity, as shown in the diagram below.
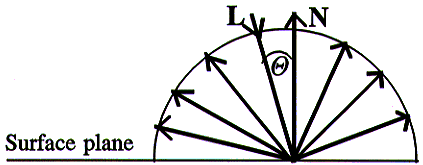
This means that the intensity of the re-radiated light is independent to the position of the viewer.
The amplitude of the re-radiated light rays is proportional to the angle at which the incident light ray strikes the surface. A greater angle of incidence will lead to a lesser amplitude of the re-radiated light rays. This effect is shown in the diagram below.
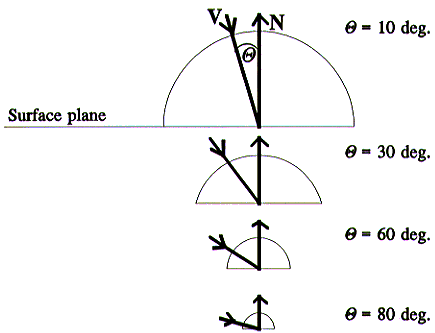
Lambert's cosine law relates the amount of reflected light to the cosine of the angle θ between the directional vector (L) to the point of the incident light ray (Lj) and the surface normal (N).
kd (kd must be in the range 0..1), the diffuse reflectance coefficient, is a measure of how much of the reflected light ray is radiated as diffusely reflected light rays.
A shiny mirror would have a diffuse reflectance of 0, while a piece of matt cardboard would probably have a diffuse reflectance of higher than 0.9
The rendering equation (for diffuse reflection) is:
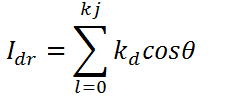
Replacing cosθ with dot product
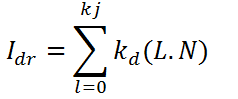
The total intensity of reflected light off a surface point is simply the addition of the specular and diffuse reflection intensities.
The intensity of light from one light source is:
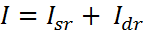
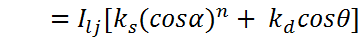
The total intensity of light for all light sources is:
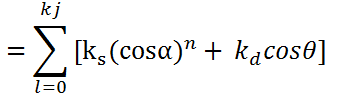
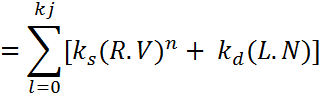
NOTE:That 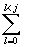 is the summation
of light sources.
is the summation
of light sources.
ks and kd are related by:
A light source will have a lesser effect on the colouring of a surface point as the distance between the light source and surface point increases.
The intensity of a light source at a point is inversely proportional to the distance squared (1/R2) between the light source and the point.
The rendering equation now becomes:
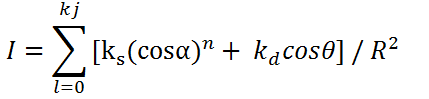
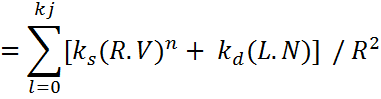
In practice, using 1/R2 does not work well with either parallel or perspective projection:
By replacing R2 with r+k, (where r is the distance, and k is a constant)
The rendering equation now becomes:
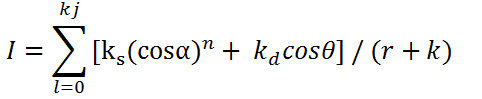
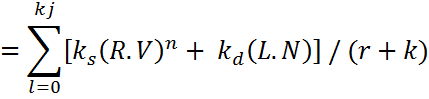
Ambient light is caused by multiple reflections of light from the various surfaces that make up a modeled environment.
Ambient light is considered to be of uniform intensity across the whole scene.
Ambient light is not dependent on the distance of a surface point from any given light source.
Even if a surface is shaded from all direct light sources, ambient light means that the surface will still contain some colour (shades of gray).
Ia is the constant for ambient light.
ka tells what percentage of the ambient light is reflected away from the surface.
The rendering equation now becomes:
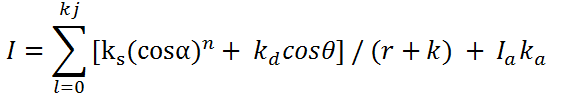
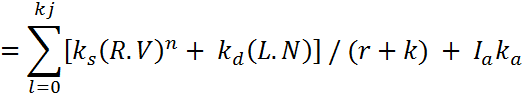
NOTE: that Iaka is not affected by the distance of the surface point from any of the light sources.
Given:
* A normalised orthographic parallel view volume
* A polygon that is defined in a clockwise direction by the three vertices:
V1 = (0.7, 0.1, 0.4)
V2 = (0.1, 0.2, 0.2)
V3 = (0.5, 0.3, 0.5)
* A single light source at position l(0.3, 0.8, 0.4)
* For the single light source:
* ks = (0.2, 0.2, 0.1)
* kd = (0.8, 0.8, 0.9)
* Ia = (0.3, 0.2, 0.1)
* ka = (0.1, 0.1, 0.1)
* k = 0.01
* n = 10
(a) Calculate the intensity of the red component of the light at the vertex V1.
Get the normal vector N
N is the cross product for the polygon.
a × b = (aY*bZ - aZ*bY, aZ*bX - aX*bZ, aX*bY - aY*bX)
a = V3 - V2
= (0.5, 0.3, 0.5) - (0.1, 0.2, 0.2)
= (0.4, 0.1, 0.3)
b = V1 - V2
= (0.7, 0.1, 0.4) - (0.1, 0.2, 0.2)
= (0.6, -0.1, 0.2)
a × b = (aY*bZ - aZ*bY, aZ*bX - aX*bZ, aX*bY - aY*bX)
= ((0.1*0.2) - (0.3*-0.1), (0.3*0.6) - (0.4*0.2), (0.4*-0.1) - (0.1*0.6))
= (0.02 + 0.03 , 0.18 - 0.08 , -0.04 - 0.06)
= (0.05 , 0.1 , -0.1)
Unit normal vector N = ((0.05 / 0.15), (0.1 / 0.15), (-0.1 / 0.15))
= (0.3333, 0.6667, -0.6667)
Other vectors
L = l - V1
= (0.3, 0.8, 0.4) - (0.7, 0.1, 0.4)
= (-0.4, 0.7, 0.0)
Unit vector L = ((-0.4 / 0.8062), (0.7 / 0.8062), (0.0 / 0.8062))
= (-0.4962, 0.8683, 0.0)
L.N = (-0.4962, 0.8683, 0.0) . (0.3333, 0.6667, -0.6667)
= 0.4135
R = 2N (L•N) - L
= 2 * (0.3333, 0.6667, -0.6667) * 0.4135 - (-0.4962, 0.8683, 0.0)
= (0.6667, 1.3334, -1.3334) * 0.4135 + (0.4962, -0.8683, 0.0)
= (0.2757, 0.5514, -0.5514) + (0.4962, -0.8683, 0.0)
= (0.7719, -0.3169, -0.5514)
Because we are using a normalised orthographic parallel view volume, the
parrallel ray that cuts through the viewport and the vertex V1 = (0.7, 0.1, 0.4) is (0.7, 0.1, 0.0)
V = (0.7, 0.1, 0.0) - (0.7, 0.1, 0.4)
Unit vector V = (0, 0, -1)
R.V = (0.7719, -0.3169, -0.5514).(0, 0, -1)
= -0.5514
(R.V)n = (-0.5514)10
= 0.0026
r = sqrt[(0.3 - 0.7)2 + (0.8 - 0.1)2 + (0.4 - 0.4)2]
= sqrt[0.16 + 0.49 + 0.0]
= sqrt[0.2657]
= 0.5155
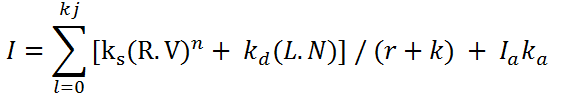 I = [0.2(0.0026) + 0.8(0.4135)] / (0.5155 + 0.01) + (0.3 * 0.1)
= [0.0005 + 0.3308] / 0.5255 + 0.03
= 0.3318 / 0.5255 + 0.03
= 0.6314 + 0.03
= 0.6614
I = [0.2(0.0026) + 0.8(0.4135)] / (0.5155 + 0.01) + (0.3 * 0.1)
= [0.0005 + 0.3308] / 0.5255 + 0.03
= 0.3318 / 0.5255 + 0.03
= 0.6314 + 0.03
= 0.6614
Copyright Derek O' Reilly, Dundalk Institute of Technology (DkIT), Dundalk, Co. Louth, Ireland.